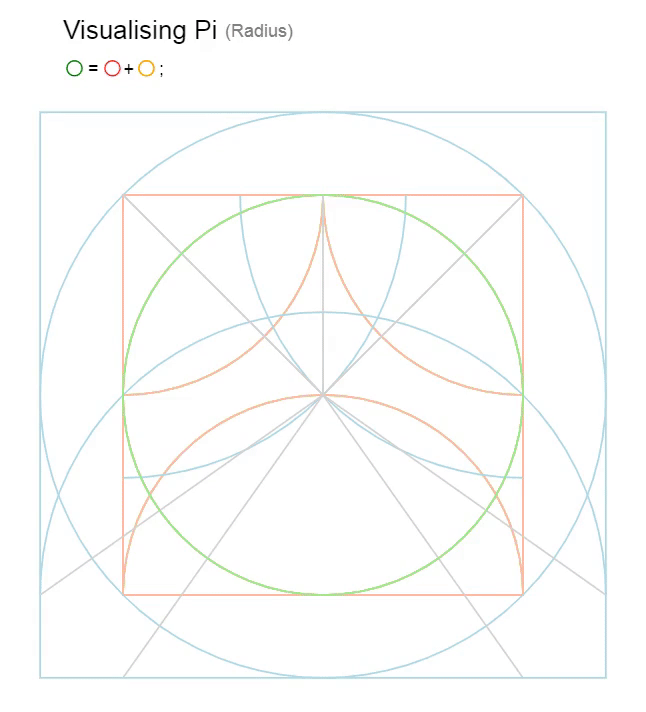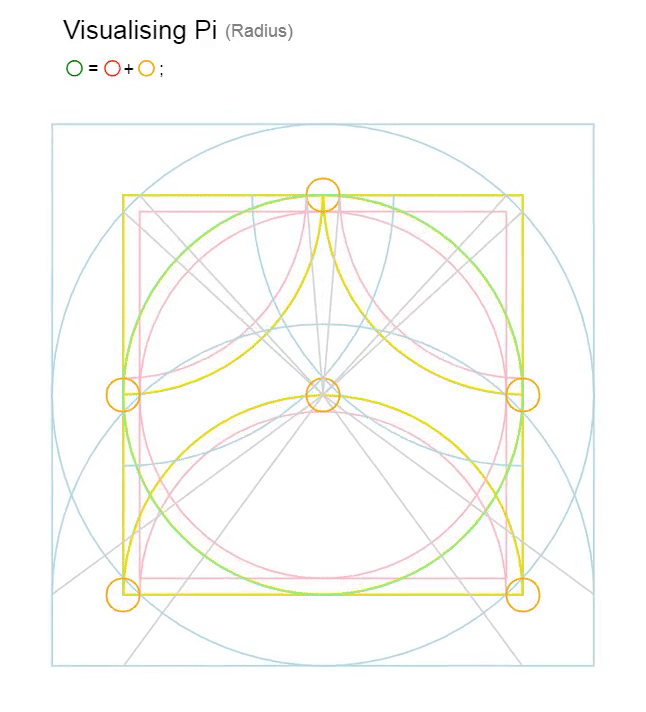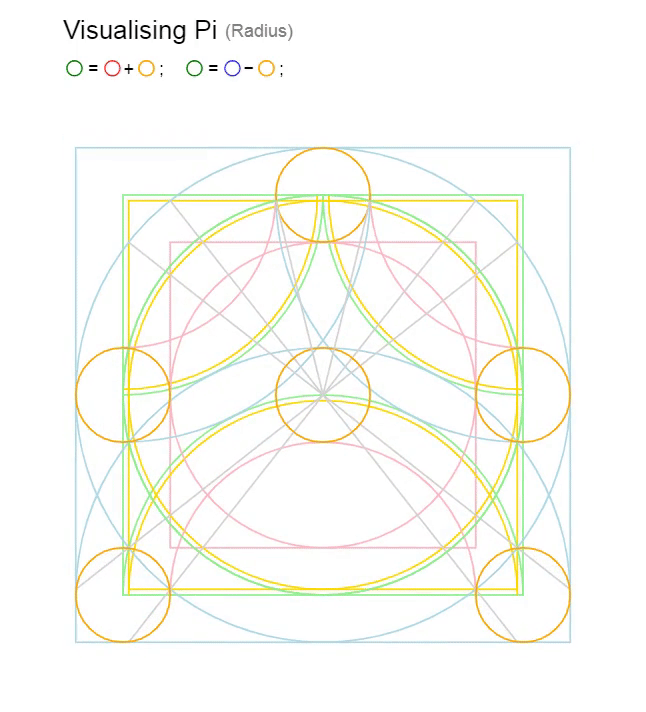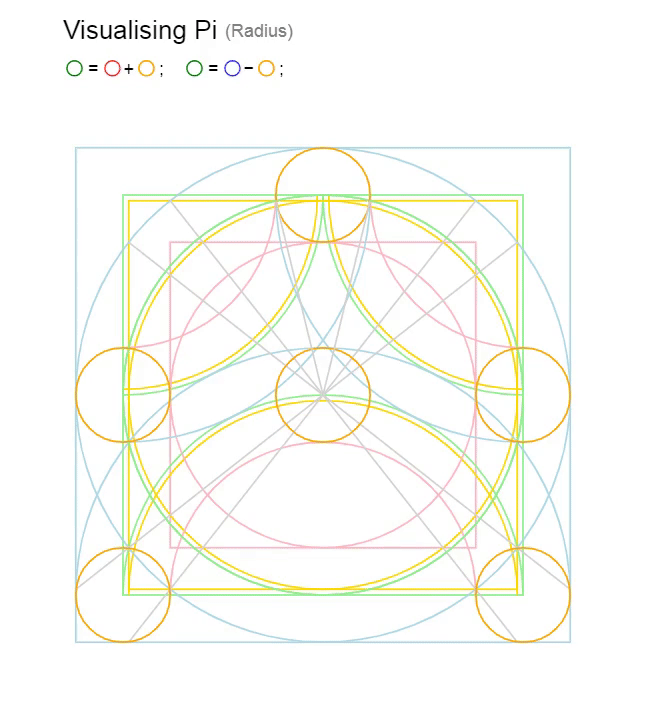The interesting cosmic geometry of the following identity is described below.

This identity allows us to unite the geometry of the circle, square and rectangle.

We start off by constructing the squares. (grey area = 4ab)

And next we add the circles as shown below.

Then we construct the blue 3-4-5 triangle. (2√(ab) = a for this example only)

The grey areas are equal.

Construct the green triangle and scale the geometry by 1/b. (assume a/b > 1)

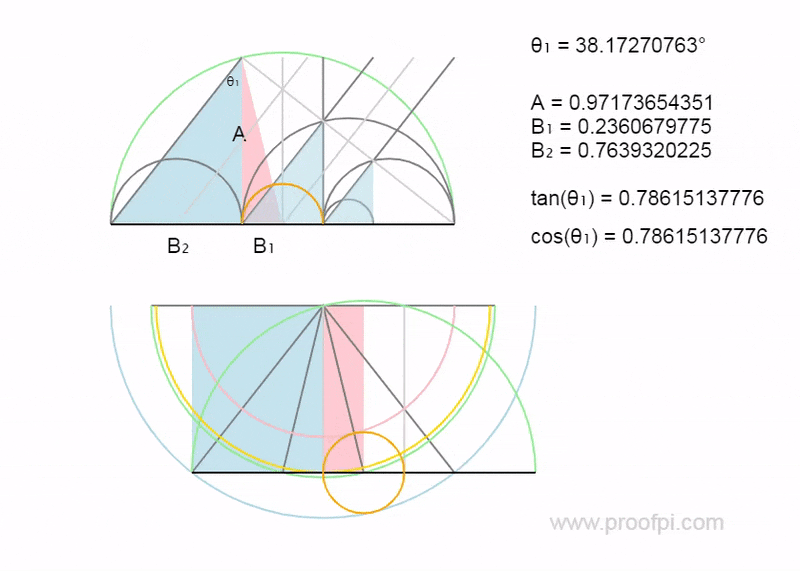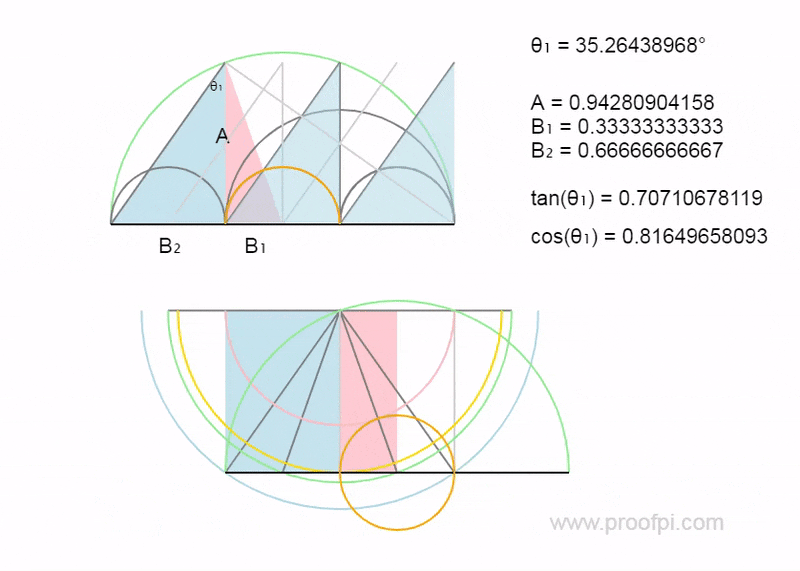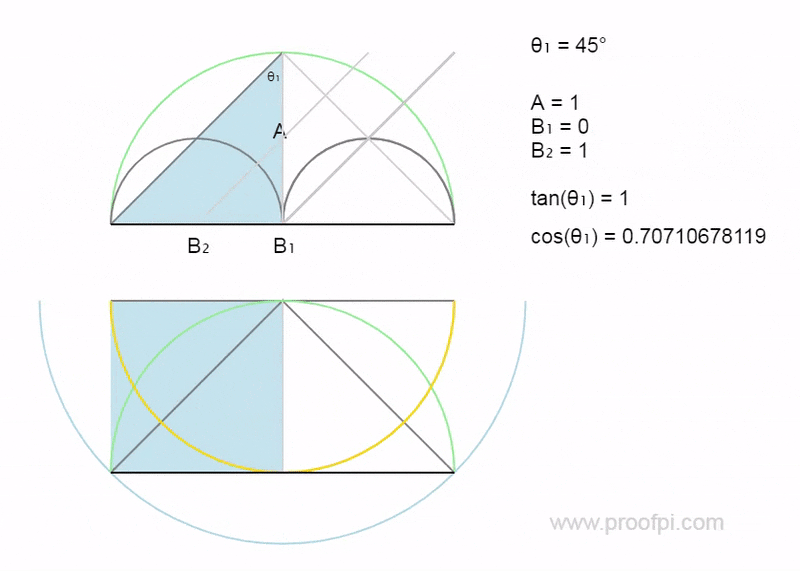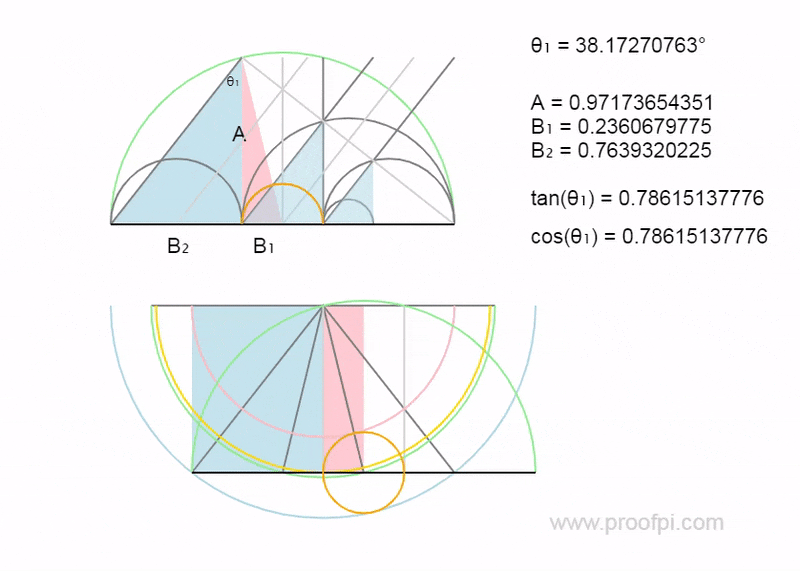
This method uses the theorem of geometry called the power of a point.

And next another example using the trusty blue 3-4-5 triangle.

The geometry of both examples shown below. (3-4-5 triangle always in blue)

The geometry of the circle.

The grey areas are always equal. (for all y)

The next example is different.

It requires another step.

We can connect the blue and olive green triangles.

The above method can be found in the geometry of both kinds folding fish.

Sophisticated Geometry/Algebra Ahead!

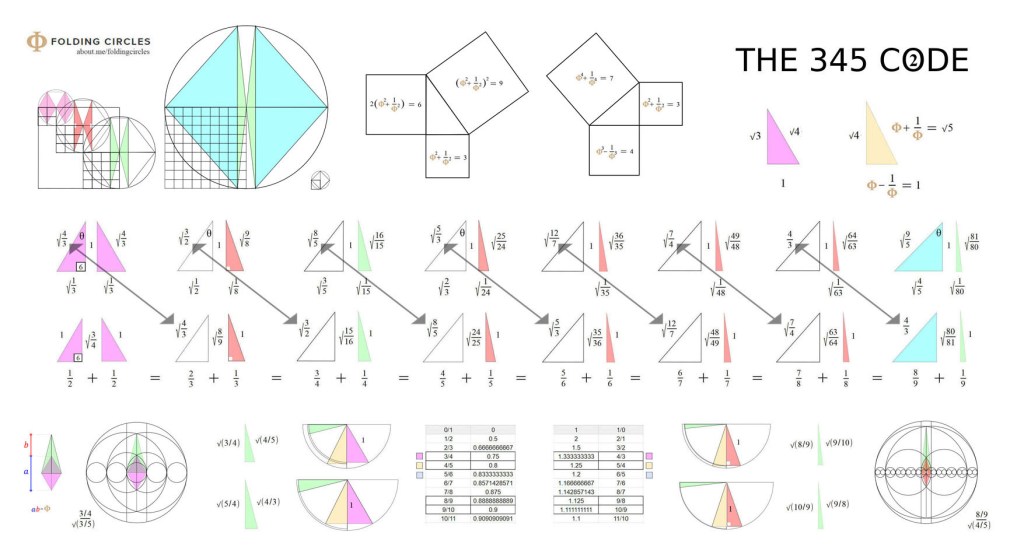
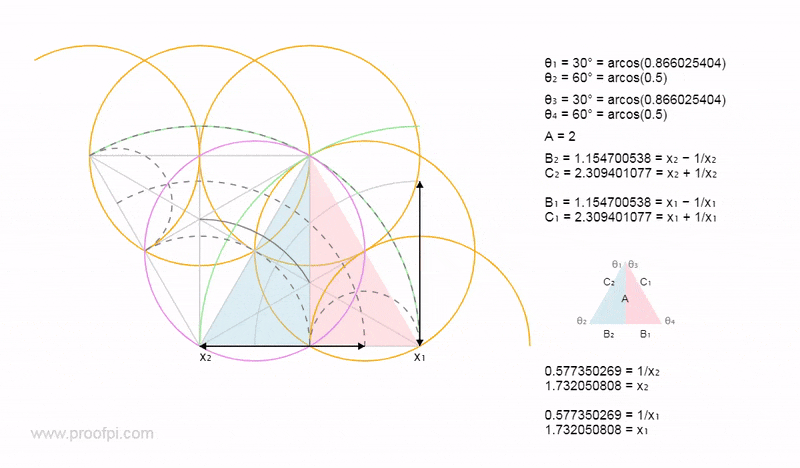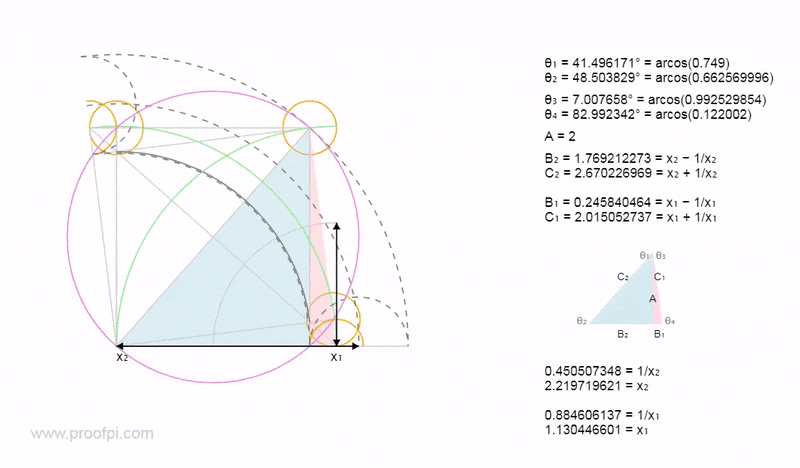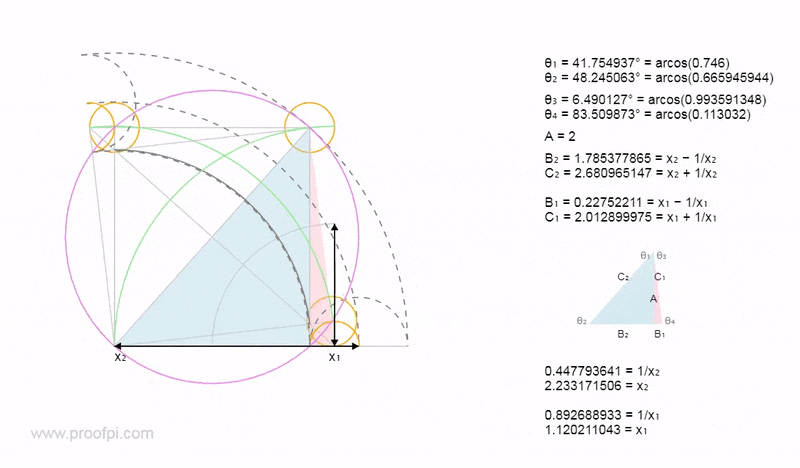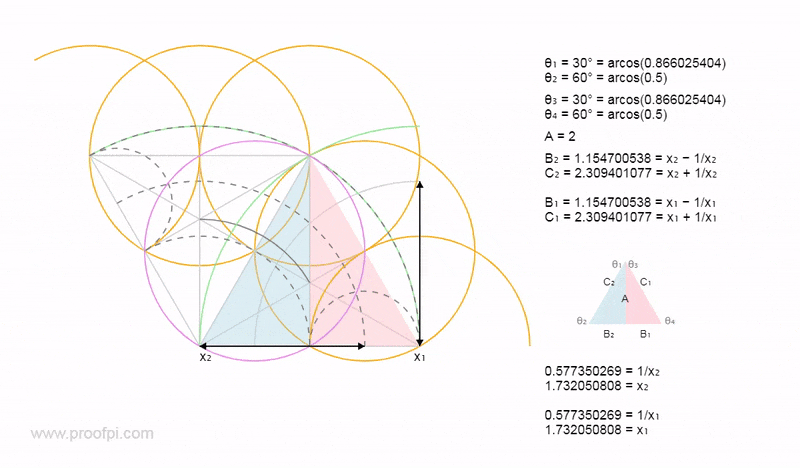
All of this geometry is directly related to the blue 3-4-5 triangle and the following values (TAN/COS/SIN) are used as variables. Yes it is extremely sophisticated.

This is difficult to understand but it is so we can track the trig values from the 3-4-5 triangle to see how they propagate through the geometric universe.

The relationship between the two y and x values. These equalities are equivalent.

Below shows the fundamental triangles all directly related to the 3-4-5 triangle.

As shown above the green triangles (y values) are related to the COS/SIN values from the 3-4-5 triangle. The red triangles (x values) are related to the TAN value.

Seven being a lucky number as we have two triangles related to the x value. (x=7)

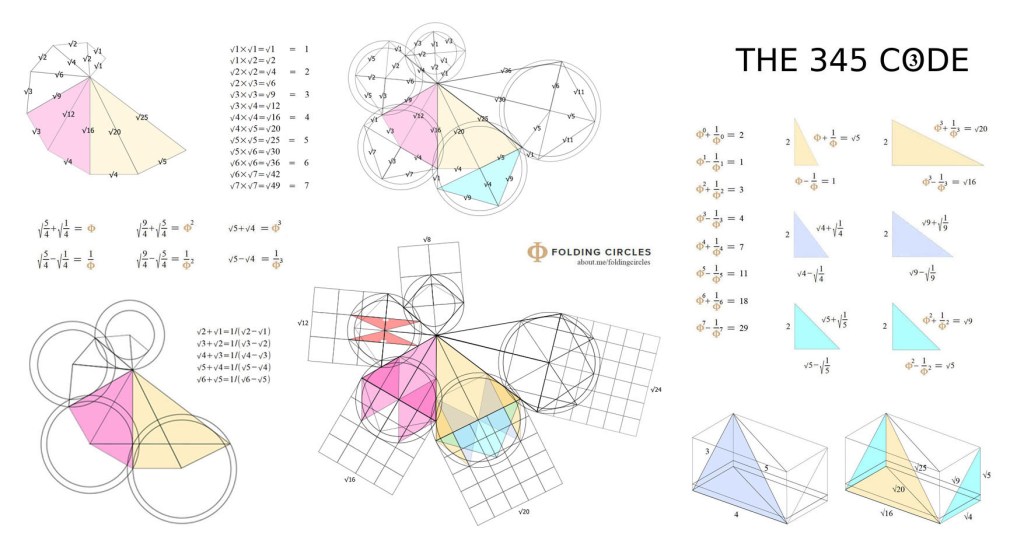
I have found two different folding fish. (square based and non-square based)

Named simply because they look like fish and they fold into a solid.

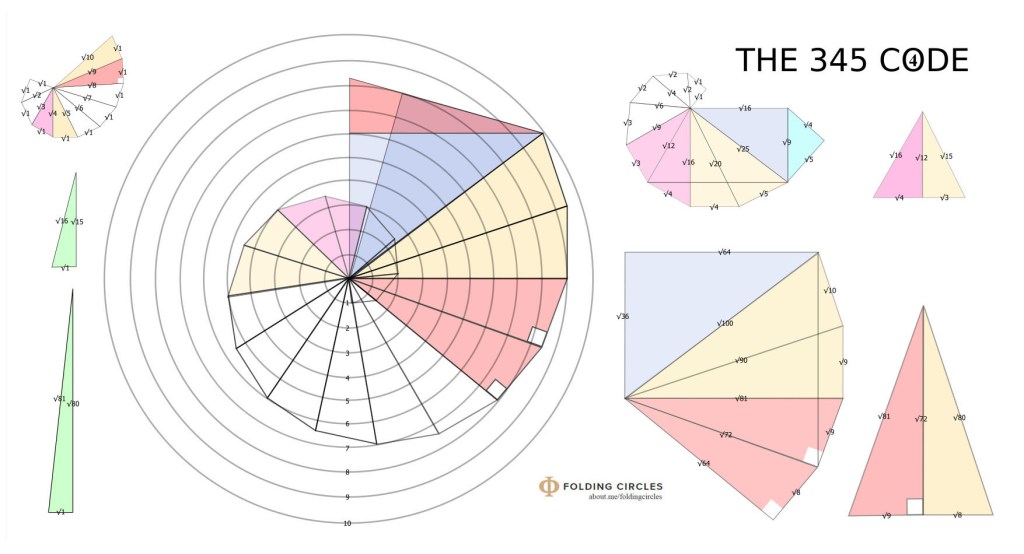
The (square based) fish live inside the well known square-root spiral while the (non-square based) fish live inside the whole number spiral. The whole number spiral has two triangles for every triangle in the square-root spiral or spiral of Theodorus.

When I say they live in the spirals I mean the conceptual roots of each fish can be found inside the two spirals and they are good ways to understand the folding fish.

These folding fish can be connected together being parts of the spiral geometry.

This nearly completes the study of the 3-4-5 triangle and its connected geometry.

“From this point onwards, things get a little bit confusing.” This cosmic (±) geometry method is mind bending and over the top on sophistication. I have been studying it for many years and if anybody is reading this, please don’t break your brain.

It takes ten years to become a master of anything and when learning geometry, remember it takes time to ‘digest’ knowledge and turn it into understanding.

I started looking at the geometry of the 3-4-5 triangle thinking it would be easy and quick and slowly found out it is secretly connected to everything (foundation stone).

Used by all ancient civilizations to construct a right-angle and famously the middle pyramid at the Giza plateau. The 3-4-5 triangle has a lot of sacred geometry to teach and shows us what we need to know to understand the great pyramid.

Joining the great pyramid and pentagon. (non-square based fish fragments)

The geometric treasure that is the golden ratio (phi) is found all the plateau but extensively in the kings chamber. In the queens chamber we find the hexagon.

Above is a comparison between the hexagon and pentagon triangles. Below shows how the geometry of the pentagon is also linked to the 3-4-5 triangle.

And next we have the intriguing geometry of the corner stone.

Being parts of the elaborate geometry of the simple square or sacred cross.

The sacred 345 triangle has many mathematical and geometric lessons to teach.

The 345 code is fascinating and shows how whole numbers are connected by an elaborate set of geometry. Follow my current progress at folding circles.

Below we can see how the numbers 1-9 are connected.

Then we can see how the 345 triangle is connected to the golden ratio and the double Spiral of Theodorus. All important triangles are given a unique colour.

Next we can see how the 345 triangle is connected to the square, equilateral triangle and the infinite spiral. Below we can see the whole numbers 1-10.

Next we see the importance of √5 and how it connects to the square and octagon.

Below the Metallic Means 1-10 and the amazing connection to the golden ratio.

This is just the tip of an infinite geometric iceberg.

The 345 triangle was revered by the Egyptians, each side given a divine name.

Also we see the geometry of the 345 triangle in many Egyptian Hieroglyphs.

The middle pyramid (Khafre) at the Giza plateau encodes a 345 triangle.

Basic Numbers using cosmic geometry.

Below the Metallic Means 1-14 showing cosmic (±) geometry and 345 triangle.

This hidden pattern in the Metallic Ratios links the 345 with the Spiral of Theodorus.

The amazing 345 triangle.

The geometry of the whole.

Folding Circles. The amazing phi.

More phi (golden ratio) using cosmic geometry.

The flower of life using cosmic geometry.

The Kingdom is within.

The amazing 345 triangle is the foundation stone. (Right angle)

Cosmic (±) geometry and shapes.

Remember, remember. (Covenant of Salt, the Sacred Hoop). Weighing scales.

The Amazing geometry of the Squared Circle.

A picture speaks a thousand words, this next picture 1001.

The geometry of the sacred 345 triangle and the number 7 (3+4=7)

This new geometry method actually makes it easier to understand.

Absolutely amazing geometry is a real brain buster.

Metallic V Organic means coming out from the magical Pythagorean spiral.

Jain pi or phi-pi is most fascinating, no other angle has this symmetry.

More geometry regarding the sacred 345 triangle.

Be water, my friend….

The Giza Plateau

The 8 sides of the Great Pyramid at Giza (3D Khufu)

The pyramids at Giza are sacred gifts of divine knowledge encoded into stone.

Exploring the amazing mystery of the Giza plateau and the three pyramids, the mathematics and geometry encoded into of the pyramids. Folding Circles.

Each square fish will fold into 1/8th of a square based pyramid, as shown below with the trusty 345 pyramid (Khafre).

The great pyramid seems to have 8 faces, visible on a solstice?

UPDATE. The geometry and mathematics of the Kings chamber.

The golden ratio (phi) is encoded into the Kings chamber. As shown above, also encoded is the 3,4,5 triangle, the 2, 3, √5 triangle and versions of the 1, 2, √5 triangle.

The queens chamber and the niche encodes the flower of life and star of David.

More geometry of the Great Pyramid, I seem to have made good progress.

Advanced Dimensions and Mathematics of the Great Pyramid.

ARCHIVE. The location of the Sphinx is related to the golden ratio (phi), as seen below.

The Egyptians used the golden ratio (phi) everywhere.

“Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio (phi). The first we may compare to a measure of gold; the second we may name a precious jewel.” Johannes Kepler

The Causeway

The causeway of Khafre and also the causeway of Khufu are the same angle and are represented by the red triangle.

Using what we learnt from Khafre to visualize the geometry of the causeway angle.

The Mathematics of the Giza Plateau

The three Great Pyramids Khufu/Cheops, Khafre/Chephren and Menkaure/Mykerinos, each seem to contain lots of mathematics.

As we will see, Khufu and Menkaure are in essence the ‘same’ pyramid just at a different scale; meaning that they both have the same angles. Khafre (the middle pyramid) is the key to understanding the mathematics of the other two pyramids.

The Three Pyramids of Giza

The mathematics of the 3 main pyramids at Giza. (3 wise men?)

• The Khafre/Chephren or middle pyramid.
• The Menkaure/Mykerinos or small pyramid.
• The Khufu/Cheops or great pyramid.

The Dimensions

When trying to find actual measurements, we find many varied numbers, so it is impossible to be 100% accurate. (numbers in feet)

• Menkaure (226, 178, 288).
• Khafre (472, 354, 590).
• Khufu (480, 378, 611).

Again, assuming the height of the Khafre relates to the number (2), we can divide the numbers by half the height of Khafre (472/2 = 236), to get the following ratios.

• Menkaure (226/236, 178/236, 288/236).
• Khafre (472/236, 354/236, 590/236).
• Khufu (480/236, 378/236, 611/236).

Interestingly the number 236 could be based on the square root of five (√5 − 2), just like the golden ratio (phi) which is found all over the Giza plateau.

If we compare the numbers, we notice a very interesting relationship between the three pyramids of Giza.

Menkaure (SUB)

• 226/236 = 0.958 compared to A₁ = 0.971 (99% accurate)
• 178/236 = 0.754 compared to B₁ = 0.763 (99% accurate)
• 288/236 = 1.220 compared to C₁ = 1.236 (99% accurate)

Khafre

• 472/236 = 2 compared to A₂ = 2 (100% accurate)
• 354/236 = 1.5 compared to B₂ = 1.5 (100% accurate)
• 590/236 = 2.5 compared to C₂ = 2.5 (100% accurate)

Khufu (SUPER)

• 480/236 = 2.033 compared to A₃ = 2.058 (99% accurate)
• 378/236 = 1.601 compared to B₃ = 1.618 (99% accurate)
• 611/236 = 2.589 compared to C₃ = 2.618 (99% accurate)

Here we can more clearly see the mathematical relationship between the three pyramids and the ‘cosmic’ equation.

The Hidden Pyramid

The amazing relationship between the three main pyramids at Giza.

• The Menkaure pyramid (A₁, B₁, C₁).
• The Khafre pyramid (A₂, B₂, C₂).
• The Khufu pyramid (A₃, B₃, C₃).
• The ‘hidden’ pyramid (A₄, B₄, C₄).

In the numbers, we find a ‘hidden’ pyramid with the same height as Khafre and the same angles (essence) as both Menkaure and Khufu.

“Simplicity is the ultimate sophistication.” Leonardo da Vinci 

Read more : The double (red and blue) triangle formation, circle and the square.

Egyptian Mathematics

For the Egyptians, it seems the ‘cosmic’ equation was most important. Probably the source of what is now called Pythagoras formula.

Two circles (1/x) and (x) interact to become two sides of a right angled triangle, with hypotenuse (x+1/x) and base (x−1/x) and with height always equal to the number (2).

Each pyramid at Giza relates to a different version of this magical equation.

This is very interesting because it gives us a different way to

They knew that the reciprocal of zero (0) was infinity ().

The Capstone

The capstone of Khufu, represents the whole of the pyramid pointing at the fractal nature of the numbers.

As above (macro, large), so below (micro, small).

The Kings Chamber

The Kings chamber contains two triangles, the 3-4-5 triangle and the 2-3-√5 triangle.

The 3-4-5 triangle is the same as the ratios of the Khafre pyramid.

Sir Flinders Petrie reported that the floor of the Kings chamber was inset from the walls, and thus the walls can exhibit two heights; one to the floor surface (17 feet) and one to the true base of the wall (19.007 feet).

The inset in the Kings chamber seems to be based on the square root of five (√5 − 2).

Possibly pointing to metallic mean (number 4).

Five and its Square Root

As we have seen, the numbers 3, 4 and 5 represent the middle pyramid and point to the ‘cosmic’ identity.

The number 5 or more precisely the square root of five (√5) is found all over the Giza plateau, lets try and find out why. As we can see below, we find the root of five in both the 1st and the 4th of the metallic means or ‘cosmic’ numbers.

1. (√5)/2 ± 1/2 = 1.618 (x) and 0.618 (1/x) where x−1/x = 1.
2. √2 ± 1 = 2.414 (x) and 0.414 (1/x) where x−1/x = 2.
3. (√13)/2 ± 3/2 = 3.303(x) and 0.303 (1/x) where x−1/x = 3.
4. √5 ± 2 = 4.236 (x) and 0.236 (1/x) where x−1/x = 4.

The nature of the square (four equal sides). Interestingly we can cut a square into both four equal triangles or squares.

Also, we can cut a square into both five equal triangles or squares.

The fractal nature of the pentagon (five equal sides).

• The Mathematics of the Giza Pyramids and Plateau.
• The Symbolism of the Giza Pyramids and Plateau.

ddd

Read more : Unknown Squared Circle