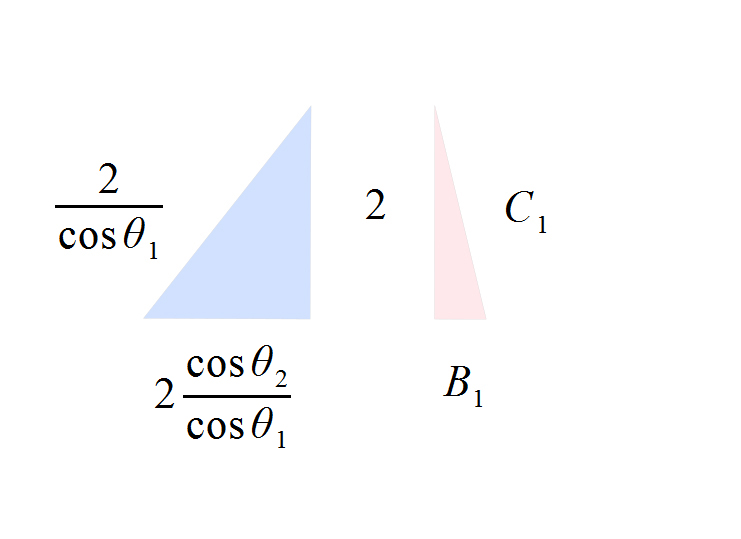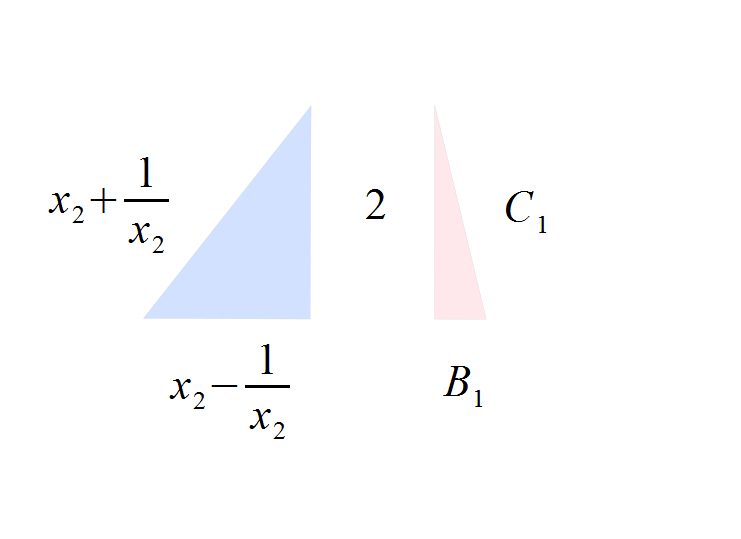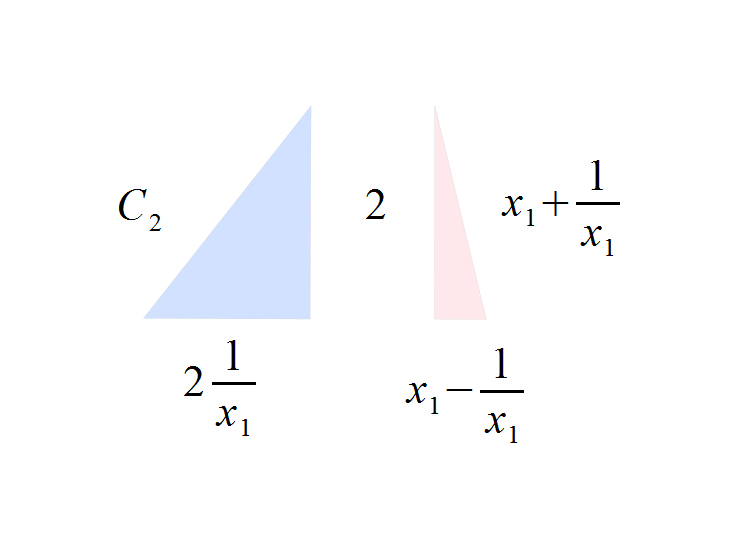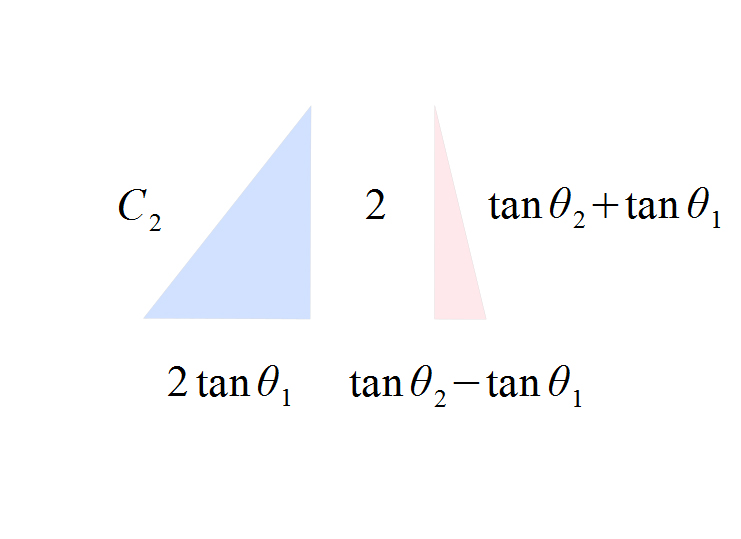These next set of circles and squares all have there areas (a) and circumferences (c) marked, along with the diameter of the circles and the height of the squares. (Fig. 13-15)

The side-length of square #1 is equal to the diameter of circle #2. The same is true for square #2 and circle #3 and square #3 and circle #4.

Also, circle #1 and square #1 have the same area. As do circle #2 and square #2, circle #3 and square #3 and circle #4 and square #4.

Also, circle #1 and square #2 have the same circumference. As do circle #2 and square #3 and circle #3 and square #4.

Next we stack all the circles and squares on top of each other.

The point marked by the triangles below is the point where the circumference of the circle and the circumference of the square are equal. (Fig. 16)

The point marked by the triangles below is the point where the area of the circle and the area of the square are equal. (Fig. 17)

The Symmetry of Pi and the Squared Circle.

We can perform simple arithmetic with both the circle and square. Meaning we can add and subtract one circle/square from another.

The symmetry the squared circle (Diameter).

The symmetry of a quarter of the Squared Circle (Radius).

Further complicated the symmetry showing both the

Further complicating the symmetry.

Square circle

More circles and squares

And another

Circles in Squares

Animation showing the process of squaring the circle.

Unifying the mathematics of the Cosmic Identity with Pythagoras and Trigonometry.

The Cosmic Identity

Pythagoras

We can link this equation with Pythagoras’s theorem.

So that for each number (x) we have a corresponding right angled triangle and each triangle has height (A) = 2, base (B) = x-1/x and hypotenuse (C) = x+1/x.

Double Triangle Formation

The following double triangle formation is found all over the geometric universe.

Originally I found it in the Vesica Piscis (a type of lens, a mathematical shape formed by the intersection of two disks).

And triangle formation in geometry.

Trigonometry

As you can see below we can unify the cosmic identity with trigonometry in the double triangle formation.

• 

• 

• 

• 

• 

Trigonometric Functions

Unifying the cosmic identity with the trigonometric function (cos) using the double triangle formation.

Unifying the cosmic identity with the trigonometric function (tan) using the double triangle formation.

These mathematics are used to visualize the angle of pi.

Visualizing the angles of and the triangles.

Tangents and Infinity

The weight of evidence for an extraordinary claim must be proportioned to its strangeness.

— Laplace.

Visualizing the angle of Pi, using the cosmic identity, Pythagoras and trigonometry.

Spinning Pi animation

Vesiica Piscis Pi Animation

Squaring the Circle Animation

Pi Buddha Animation

Pi slideshow animation